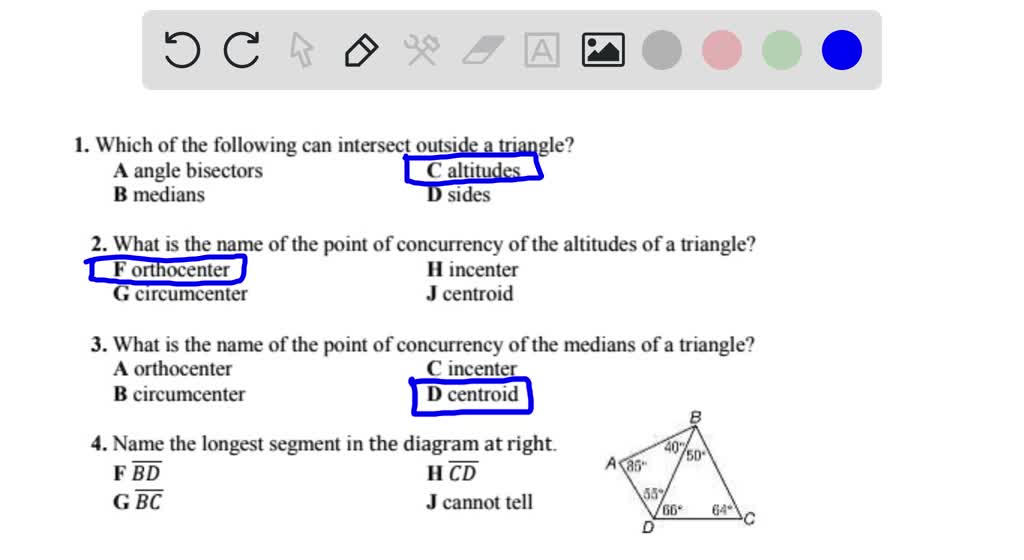
Which of the Following Can Intersect Outside a Triangle

1063 AB is a chord of length 1 6 c m of circle of radius 1 0 c m. What is the Orthocenter of.

Solved Which Of The Following Can Intersect Outside Triangle Angle Bisectors Altitudes B Medians D Sides 2 What Is The Name Of The Point Of Concurrency Of The Altitudes Of A Triangle F

Let us have a focus on some of the significant properties of the orthocenter.

. Some orthocenters can be found on the outside of a triangle Incenter. Although triangles more frequently predict a. Unlike other chart patterns which signal a clear directionality to the forthcoming price movement triangle patterns can anticipate either a continuation of the previous trend or a reversal.

Notice from the proof of Theorem 25 that the center O was on the perpendicular bisector of one of the sides overlineAB. When all right bisectors of a triangle intersect each other at a common point that point has its own coordinates that are related to the coordinates of all the three vertices of the triangle. 222 in The 45-45-90 triangle also referred to as an isosceles right triangle since it has two sides of equal lengths is a right triangle in which the sides corresponding to the angles 45-45-90 follow a ratio of 11 2.

Cathetus of the triangle. The word diagonal derives from the ancient Greek διαγώνιος diagonios from angle to angle from διά- dia- through across and γωνία gonia angle related to gony knee. Given two line segments p1 q1 and p2 q2 find if the given line segments intersect with each other.

Building a min heap takes On time and every extract min operation takes OLogn time See this. Similar arguments for the other. Each side of the line segment should intersect with another line segment only at its endpoint.

See the following triangle. We need a different procedure for acute and obtuse triangles since for an acute triangle the center of the circumscribed circle will be inside the triangle and it will be outside for an obtuse triangle. Remember that the centroid divides each median in a ratio of 21.

An altitude or height is each of the perpendicular lines drawn from one vertex to the opposite side or its extension. The RUN is one-half the span. Point H is the orthocenter of this triangle because it is the point where all the three altitudes of the triangle are intersecting each other.

The centroid of an equilateral triangle can readily find as it is always located inside the triangle like the incenter another one the triangles concurrent points. Concurrency of the angle bisectors of a triangle. Before we discuss solution let us define notion of orientation.

View solution In Fig. The orthocenter can be inside acute triangle outside obtuse triangle or on right triangle the triangle. The following pseudocode doesnt use heap.

Find the length of PA. Throughout the article you will learn about centroid definition the centroid of an equilateral triangle with solved examples properties of triangles and more. Triangle patterns are a chart pattern commonly identified by traders when a stock prices trading range narrows following an uptrend or downtrend.

A triangle and it divides each median into a ratio of 21 vertex to centroid. The orthocenter is. The span is the length from the outside wall to the outside wall of a building.

Specialized terms help to explain the triangle relationships in roof construction. In the following diagram PA and PB are tangents to the circle. The centroid of a triangle can be defined as the point of intersection of all the three medians of a triangle.

Next lets look at angle bisectors. So technically the height does not necessarily intersect with the base. Concurrency of the three altitudes of a triangle.

Also in step 1 instead of sorting we can use min heap data structure. A polygon should have at least three sides. Find the value of A O B.

Derivation of the Area of a Triangle from Rectangle. Based on the number of sides of a polygon we can easily identify the shape of the polygon. The following diagram shows different possible orientations of.

Because construction is often made up of multiple layers of wood building plans often provided detailed descriptions to make clear where to begin or end measurements. Play around with our applet to see how the area of a triangle can be computed from any baseheight pairing. A right triangle or right-angled triangle has one of its interior angles measuring 90 a right angleThe side opposite to the right angle is the hypotenuse the longest side of the triangleThe other two sides are called the legs or catheti singular.

Orientation of an ordered triplet of points in the plane can be counterclockwise clockwise collinear. The circumcenter however is also said to be the centre of the circumcircle of a triangle which can. With a Self-Balancing BST we can do all of the above operations in OLogn time.

In other words we can say that the point of concurrency of the bisector of the sides of a triangle is termed the circumcenter. The picture below shows you that the height can actually extend outside of the triangle. An orthocenter finder generates the absolute values of these coordinates within seconds.

Triangles can also be classified according to their internal angles measured here in degrees. Here a minute refers to 160th of a degree. You can convert angle units here.

The circumcentre of a triangle is specified as the point where the perpendicular bisectors of the sides of a given triangle intersect or meet. View solution Tangents PA and PB drawn to x 2 y 2 9 from any arbitrary point P on the line x y 2 5. It simply sort the array.

The tangents at A and B intersect at point P. Centroid to midpoint 21. These are lines drawn from an angle that bisect the angle or splits it.

What is the area of the triangle pictured. It was used by. Angle of incidence θi Angle of refraction θr Critical angle.

For example a three-sided polygon is a triangle and a five-sided polygon is called a pentagon. The centroid of a triangle distributes all the medians in a 21 ratio. In geometry a diagonal is a line segment joining two vertices of a polygon or polyhedron when those vertices are not on the same edgeInformally any sloping line is called diagonal.

The point where all the three altitudes of the triangle meet or intersect each other. More specifically the centroid will always be 23 of the way with any given median towards the vertex and 13 towards the side.

Ap Board 9th Class Maths Solutions Chapter 4 Lines And Angles Ex 4 4 Ap Board Solutions In 2022 Maths Solutions Math Chapter

Solved Which Of The Following Can Intersect Outside Triangle Angle Bisectors Altitudes B Medians D Sides 2 What Is The Name Of The Point Of Concurrency Of The Altitudes Of A Triangle F

Lines Segments That Intersects Circle Tangents Secants Chords High School Geometry Segmentation Geometry High School Number Sense